ACI Building Code Requirements and Safety Provisions

ACI Code Safety Provisions for reinforced buildings
Structural members must always be proportioned to resist loads greater than service or actual loads, in order to provide proper safety against failure. In the strength design method, the member is designed to resist the factored loads which are obtained by multiplying the factored loads with live loads.
Different factors are used for different loadings. As dead loads can be estimated quite accurately, their load factors are smaller than those of live loads, which have a high degree of uncertainty. Several load factor conditions must be considered in the design to compute the maximum and minimum design forces. Reduction factors are used for some combinations of loads to reflect the low probability of their simultaneous occurrences. Now if the ultimate load is denoted by U, the according to the ACI code, the ultimate required strength U, shall be the most critical of the following:
Basic Equation U = 1.2D + 1.6L
In addition to the load factors, the ACI code specifies another factor to allow an additional reserve in the capacity of the structural member. The nominal strength is generally calculated using accepted, analytical procedures based on statistics and equilibrium. However, in order to account for the degree of accuracy within which the nominal strength can be calculated and for adverse variations in materials and dimensions, a strength reduction factor Phi should be used in the strength design method. Values of the strength reduction factor (Phi) are:
For flexure of tension controlled sections Phi = 0.9
For shear and torsion Phi = 0.75
For compression members with spiral reinforcement Phi = 0.70
For compression members with laterla ties Phi = 0.65
Nominal strength
Actual strength from the material properties is called the nominal strength.
Nominal x Phi = Design strength
As safe design is achieved when the structural strength obtained by multiplying the nominal strength by the reduction factor phi , exceeds or equals the strength needed to withstand the factored loads.
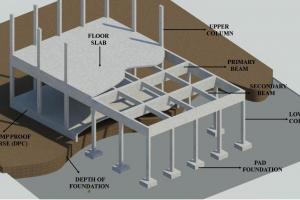
| Design process is the reverse of loading. Design starts from the foundation , unlike the load which transfers to the foundation only at the end. |
where
Mu, Vu and Pu equals external factored moments, shear forces and axial forces.
Mn, Vn and Pn equals the nominal moment, shear and axial capacity of the member respectively